2025. 8. 16. 19:10ㆍ카테고리 없음
마음의 고향같은 부스트캠프 AI Tech 의 프리코스 에서 다룬 딥러닝 학습에 이용되는 수학적 개념들을 정리해 보았습니다.
강의가 입문자를 대상으로 하는 만큼 핵심만 다루고, 수식들은 최대한 자연어로 풀어보았습니다.
[부스트캠프 AI Tech 프리코스] 인공지능 기초 다지기 (1)
[부스트캠프 AI Tech 프리코스] 인공지능 기초 다지기 (2)
확률론
실제 존재하는 데이터의 분포를 학습하여 새로운 데이터에서 가장 높은 성능을 보이기 위하여 확률론을 도입했습니다.
다양한 loss function 들이 확률론적 원리로 유도됩니다
확률분포
확률분포는 "데이터의 초상화" 입니다. 해당 데이터가 가지는 특성에 따라 이산확률분포와 연속확률분포로 나눌 수 있습니다.
이산확률분포
넓은 범위에서 "분류" 로 정의될 수 있는 task 들은 이산확률분포로 모델링합니다. 이산확률분포는 가능한 경우의 수를 모두 더해서 모델링합니다. 단순한 이진분류(binary classification) 뿐 아니라 다음에 나올 token를 찾는 NLP/LLM 계열, 이미지의 라벨을 찾는 분류 또한 이산확률분포를 이용한다고 볼 수 있습니다.

P(X=x) 는 확률질량함수로 확률변수 X가 정확히 x 값을 가질 확률을 뜻합니다.
표본공간 (모든 발생 가능한 경우) 에 대한 확률질량함수를 더하면 1이 됩니다.
윷놀이로 예시를 들어 보겠습니다.
윷놀이는 이항분포라는 분포를 따르고, 도,개, 걸, 윷, 모가 나올 확률은 각각 아래와 같습니다.
따라서 모든 경우의 확률을 더하면 100%가 채워집니다.
| 발생 확률 | |
| 도 | 25% |
| 개 | 37.5% |
| 걸 | 25% |
| 윷 | 6.25% |
| 모 | 6.25% |
연속확률분포
넓은 범위에서 "회귀" 로 정의될 수 있는 task 들은 연속확률분포로 모델링합니다. 연속확률분포는 덧셈 대신 확률변수의 밀도를 적분해서 표현합니다. 가격 등의 수치 추정은 이산적이지 않기 때문에, 연속확률분포를 이용한다고 볼 수 있습니다.

이산확률분포와 똑같은 원리로 덧셈을 수행... 하고 싶지만 덧셈으로는 연속된 공간을 설명하는 데 한계가 있기 때문에 적분을 사용합니다.
적분이 부담스럽다면 우선은 "넓이를 구하는 방법" 이라고만 개념적으로 생각해주셔도 될 것 같습니다.
몬테카를로 샘플링
확률분포를 알지 못하는 상황에서 데이터가 iid(independent and identically distributed) 로 샘플링 되었을 때 기대값을 계산하는 방법입니다. 기계학습에서는 데이터만 주어지고 어떤 분포를 가지는지는 알 수 없는 상황이 많은데, 이때 몬테카를로 샘플링은 iid가 보장될 때 큰 수의 법칙에 의해 수렴을 보장하게 됩니다.

식이 좀 복잡하게 생겼는데, 실제로는 단순히 샘플들의 산술평균을 구하는 것입니다.이 식의 좌변은 우리가 구하고 싶은 진짜 기댓값이고, 우변은 N개의 샘플 데이터들에 함수 f를 적용한 값들의 평균으로 근사하는 것을 의미합니다.
통계학
조건부확률 vs 가능도
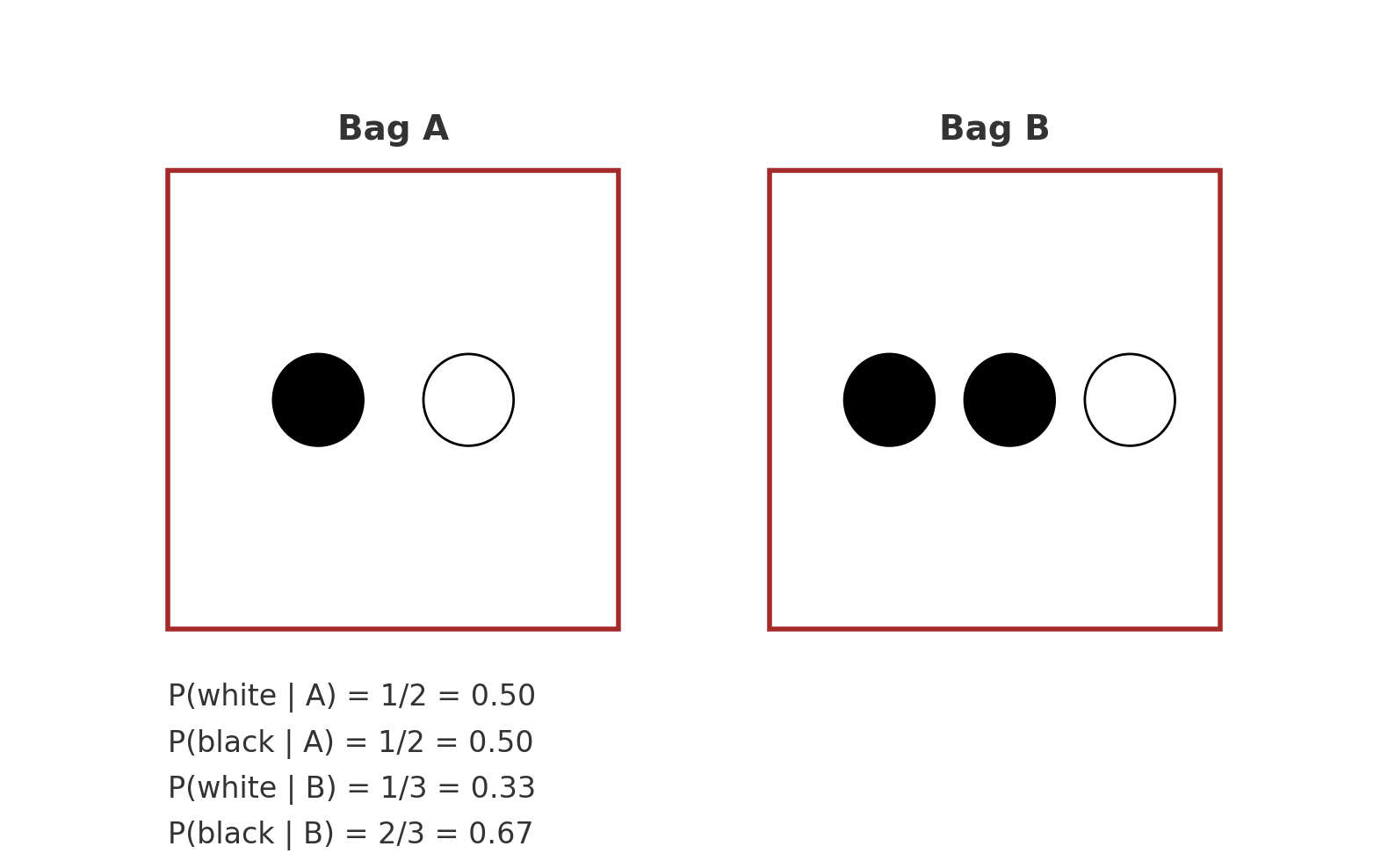
조건부확률 P(B|A) 는 사건 A가 발생했을 때 사건 B가 발생할 확률을 나타냅니다.

이 조건부확률을 입력변수 x와 정답 y에 대해서 해석하게 되면
P(x|y) 는 정답 y 가 주어진 상황에서 입력 변수 x의 분포를,
P(y|x) 는 입력 변수 x 가 주어진 상황에서 y가 정답일 확률을 찾게 됩니다.
위 그림에서 P(흑|A) = 1/2 (A주머니를 골랐을 때 흑돌이 나올 확률은 1/2),
P(백|A) = 1/2 (A주머니를 골랐을 때 백돌이 나올 확률은 1/2) 입니다.
이미지 분류 task로 확장하게 되면 x가 이미지, y가 정답(고양이) 인 상황에서
P(y|x) 는 "이미지가 주어졌을 때 고양이일 확률을 구하는 방법" 으로 해석합니다.
이와 비슷하지만 가능도(likelihood, 우도) 는 주어진 관측값 x가 확률분포 y 로부터 나왔을 확률입니다
이산확률분포에서는 L(θ|x) = P(X = x|θ)
연속확률분포에서는 L(θ|x) = f(x|θ)
위 그림에서는 반대로 주머니에서 흑돌을 꺼냈을 때 꺼낸 주머니가 B주머니일 확률을 계산하는 경우가 됩니다.
따라서 한 데이터셋 안에서 모든 가능도를 더했을 때 1(100%) 가 되는 것을 보장하지는 않습니다.
모수
다양한 종류의 확률 분포에서, 분포의 형태와 특성을 설명하는 hyperparameter 입니다.
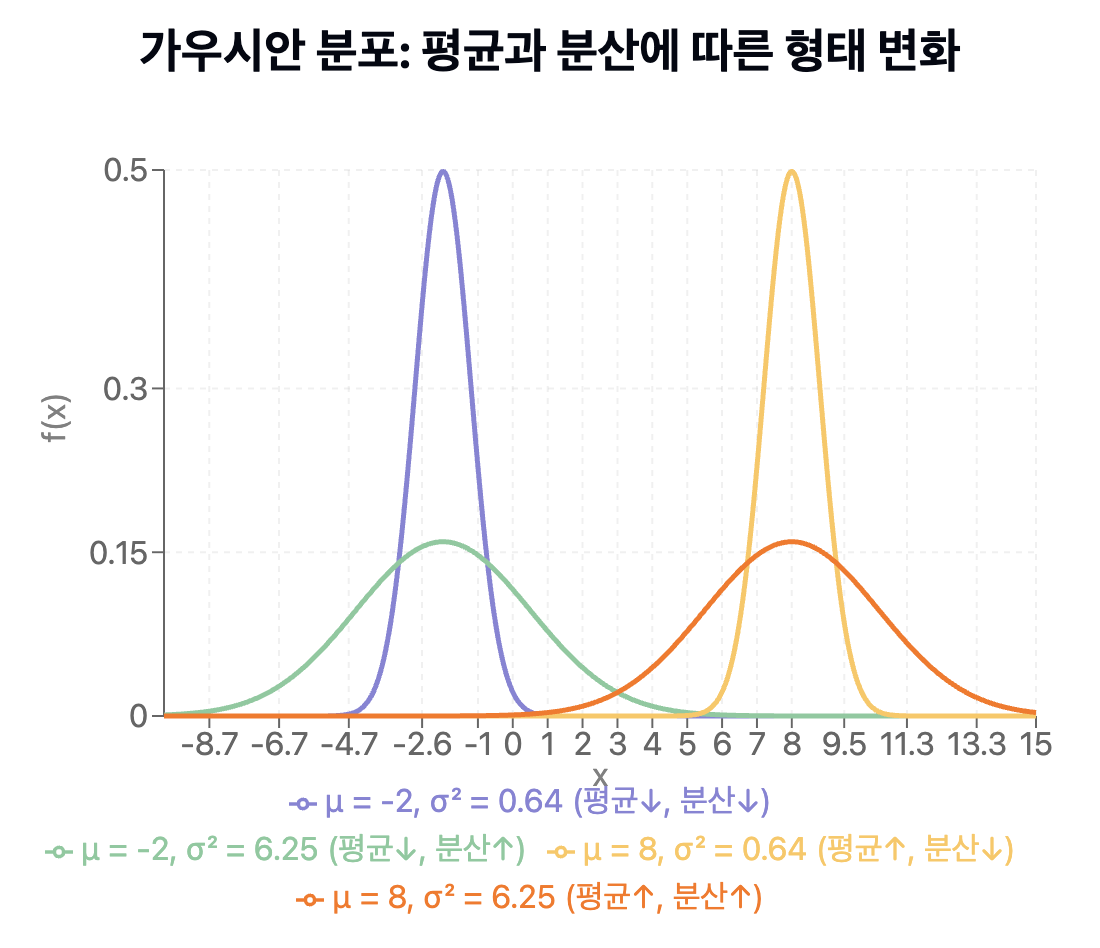
대표적으로 정규분포(Gaussian Distribution)는 평균(μ) 과 분산(σ²) 을 모수로 가집니다.
아래 그림처럼 같은 정규분포를 가지고도 평균과 분산의 변화에 따라 다양한 데이터 분포를 나타낼 수 있습니다.
모수를 구하는 방법 - 최대가능도 추정법 (max likelihood estimation)
위에서 다뤘듯 가능도(likelihood) 는 주어진 관측값이 특정 확률분포로부터 나왔을 확률입니다. 따라서 현재 데이터를 설명하는 확률분포, 그 중에서도 확률분포를 정했다는 가정 하에 모수를 찾기 위해 사용하는 방법이 최대가능도추정법 입니다.
말 그대로 가능도(likelihood) 를 가장 크게하는 것이 목표인데, 대부분의 최적화 함수가 최소화를 목적으로 하기 때문에 음수를 취하고, 연산을 단순화하기 위해서 log를 취해서 Negative Log Likelihood를 찾게 됩니다.
베이즈 통계학
베이즈 정리는 사전 지식과 새로운 증거, 조건부 확률을 사용하여 지식을 업데이트 하는 방법입니다.
그렇다고 베이즈 정리가 인과관계를 보장하는 것은 아닙니다.

조건부확률 예제
COVID-99 의 발병률이 10% 로 알려져있다. COVID-99 에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1% 라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99 에 감염되었을 확률은 무엇일까요?
이 문제에서 θ는 "코로나 감염", D는 "감염으로 검진됨" 으로 해석할 수 있습니다. 문제를 수식화 해 보면
사전확률인 코로나의 발병률은 P(θ) = 0.1
코로나 감염 시 감염으로 진단될 확률인 P(D|θ) = 0.99
코로나 미감염 시 감염으로 진단될 확률 P(D|not θ) = 0.01 일 때
코로나 진단 시 감염일 확률 P(θ|D) 를 찾으면 됩니다.
P(θ|D) 를 찾기 위해 방금 소개된 베이즈 정리 식을 이용하려 합니다.
우변 중 현재 우리가 알지 못하는 값은 P(D) 뿐인데, P(D|θ) 와 P(D|not θ) 를 활용해 수식을 조작하면 찾을 수 있습니다. 우리는 맨 위에서 조건부확률 식을 다뤘으니까요!
블로그 에디터에서 수식을 다루기가 쉽지 않아서 풀이과정을 사진으로 첨부했습니다 하하
추론된 사후확률인 코로나 검진시 감염일 확률 P(θ|D) = 91.6% 이고
(감염 여부와 무관하게) 코로나로 진단될 확률 P(D) = 10.8% 입니다.

입문할 때 수학적 개념이 진입장벽처럼 작용하는 경우가 많은데, 조금이나마 도움이 되면 좋겠습니다 ☺️